Curva de nível
Origem: Wikipédia, a enciclopédia livre.
 Nota: Se procura o sistema de cultivo, veja Curva de nível (agricultura).
Nota: Se procura o sistema de cultivo, veja Curva de nível (agricultura).Exemplo de mapa topográfico com curvas de nível a representar o relevo.
Numa planta topográfica, uma curva de nível caracteriza-se como uma linha imaginária que une todos os pontos de igual altitude de uma região representada. É chamada de "curva" pois normalmente a linha que resulta do estudo das altitudes de um terreno são em geral manifestadas por curvas.
São associadas a valores de altitude em metros (m)
Portanto, a curva de nível serve para identificar e unir todos os pontos de igual altitude de um certo lugar.
Esta pode ser interpretada como uma batata, se a cortarmos em camadas, depois gradualmente desenharmos cada "camada" da batata em uma folha de papel, poderemos interpretar o desenho como uma planta de altitudes de um lugar. Se repetirmos o acto varias vezes no mesmo papel poderemos unir os pontos de iguais altitudes formando uma curva de nível.
As curvas de nível indicam uma distância vertical acima, ou abaixo, de um plano de referência de nível. Começando no nível médio dos mares, que é a curva de nível zero, cada curva de nível tem um determinado valor. A distância vertical entre as curvas de nível é conhecida como equidistância, cujo valor é encontrado nas informações marginais da carta topográfica.
Categorias: Topografia | Cartografia | Geomática
Fonte:
http://pt.wikipedia.org/wiki/Curva_de_nível
Formas de relevo e curvas de nível
Junho 9, 2007 por pedrotildes
As curvas de nível dão informação de altitudes. No entanto, a sua configuração dá-nos informações muito precisas do relevo. Para se poder ter uma leitura correcta do relevo a partir das curvas de nível deixo aqui algumas pistas:
a) Curvas de nível mais próximas significam declives mais elevados, enquanto que curvas de nível mais afastadas representam áreas de declives mais suaves;
b) curvas de nível concêntricas com os valores mais elevados no centro representam montanhas ou montes. Se no centro estiverem, ao contrário valores mais baixos, então temos uma área deprimida.
c) A melhor forma de tirar dúvidas é fazer um perfil topográfico
Vejamos alguns exemplos
Neste caso temos dois conjuntos de curvas concêntricas que formam dois cumes relativamente arredondados. Mas, no cume da direita, as altitudes são mais elevadas e os declives são mais acentuados na vertente direita. A altitude entre os dois cumes está compreendida entre os 20 e 30 metros. Repara que a curva de nível dos 20m não “fecha”.
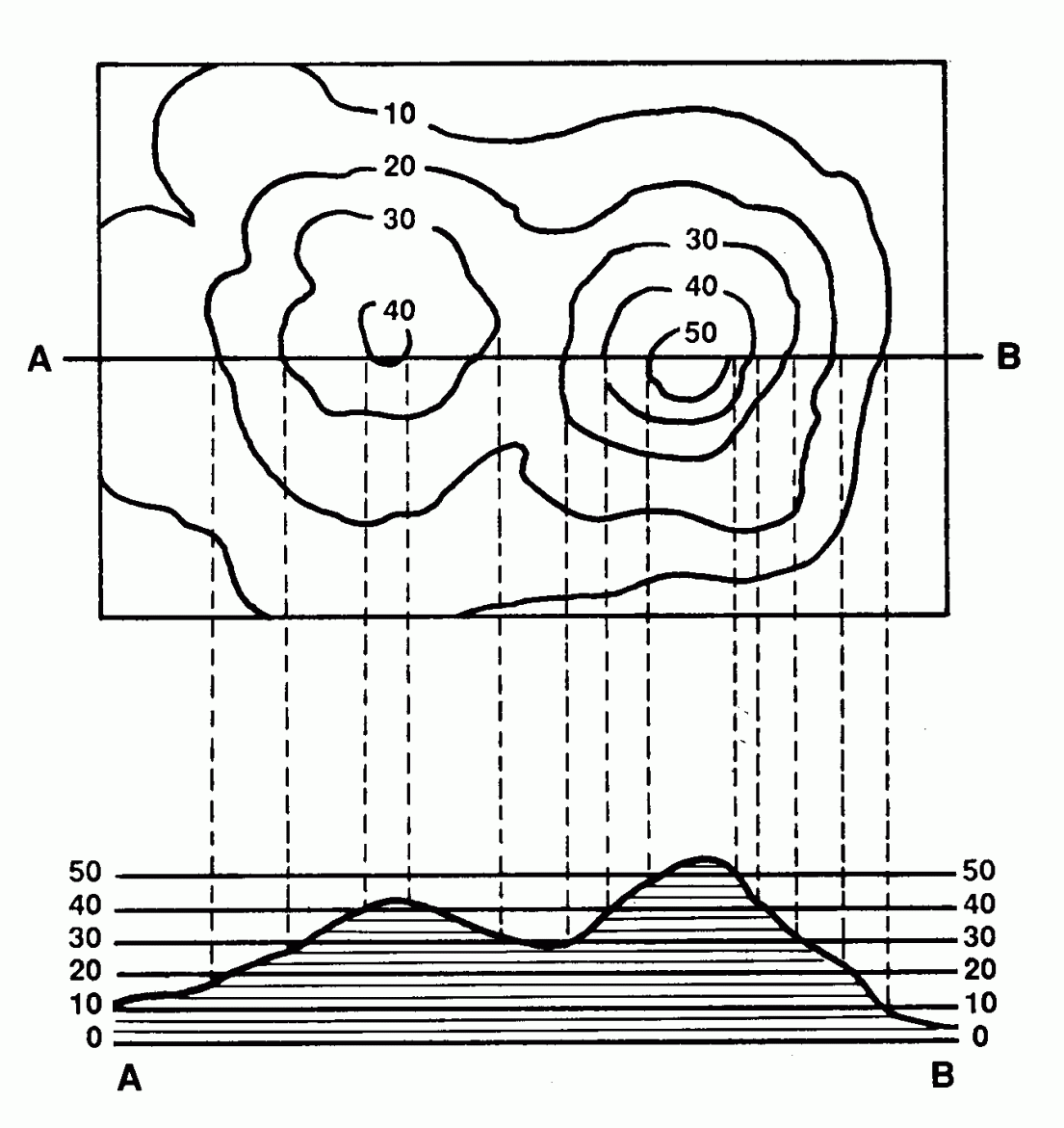
O exemplo em cima mostra um perfil topográfico mais complexo. temos duas montanhas com formas muito distintas. A da esquerda tem maiores altitudes, tem um cume mais pontiagudo, maiores declives e alguma assimetria. A sua vertente direita tem maiores declives que a vertente da esquerda, como se pode ver no perfil e nas curvas de nível que estão mais juntas. O cume da esuqerda tem uma forma mais arredondada, menores altitudes, mas continuamos na presença de um relevo assimétrico: há uma difderença de declives entre as duas montanhas.
Fonte:
http://geographicae.wordpress.com/2007/06/09/formas-de-relevo-e-curvas-de-nivel/
Topografia (1)
Hipsometria e curvas de nível
Cláudio Mendonça*
Especial para Página 3 Pedagogia & Comunicação
É possível representar as diferentes altitudes de um terreno de duas formas: por meio da hipsometria e por meio de curvas de nível.
Em mapas de pequena escala, empregados para o mapeamento de grandes áreas, utiliza-se a hipsometria. Os estudos hipsométricos possibilitam conhecer o relevo de uma região de forma mais aprofundada e, também, quais são os fenômenos que se processam em sua superfície.
Trata-se de uma operação voltada a medição de altitudes dos pontos de um terreno e a representação dessas altitudes numa planta topográfica. No método hipsométrico, as altitudes de uma região são apresentadas por diferentes cores. Geralmente utiliza-se um sistema de graduação de cores (cores hipsométricas).
As cores não são aleatórias, mas obedecem a uma convenção - o marrom (ou alaranjado) mais escuro representa as maiores altitudes (montanhas, serras, cordilheiras, chapadas), cuja tonalidade vai clareando conforme diminuem as altitudes; o amarelo representa médias altitudes (geralmente planaltos) e o verde, as baixas altitudes (planícies). As águas continentais (rios, lagos) e marítimas se representam em azul - quanto mais carregada for a tonalidade do azul nos mares e oceanos mais profundos eles são.

Em mapas de maior escala, a altitude é representada por meio de curvas de nível. Trata-se de linhas traçadas sobre o mapa e separadas entre si por intervalos constantes de altitude. Uma curva de nível caracteriza-se como uma linha imaginária que une os pontos de igual altitude de uma região apresentada.
É chamada de 'curva' uma vez que a linha que resulta do estudo das altitudes de um terreno é em geral manifestada por curvas. Portanto, quando uma linha está muito distante de outra, o terreno apresenta um declive suave, e quando as linhas estão muito próximas entre si, apresenta declive bastante acentuado, ou seja, curvas de nível mais próximas significam declives mais elevados, enquanto curvas de nível mais afastadas representam áreas de declives mais suaves.
Há ainda o caso das curvas de nível concêntricas, cujos valores mais elevados no centro representam montanhas ou montes (imagem à esquerda). Se no centro estiverem, ao contrário valores mais baixos, então tem-se uma área com depressões (imagem à direita):

Com as curvas de nível são construídos mapas topográficos e sua correta representação e interpretação, permite obter uma visão tridimensional do relevo. As curvas de nível transformam uma representação bidimensional em tridimensional.
Fonte:
http://educacao.uol.com.br/geografia/ult1701u69.jhtm
Topografia (2)
Propriedade das curvas de nível e perfil topográfico
São propriedades das curvas de nível:
Todos os pontos situados sobre uma curva tem a mesma ou altitude;
Duas curvas de nível não podem se tocar ou se cruzar - caso isso ocorra, será resultado de um efeito visual, uma vez que na verdade uma curva passa por baixo da outra, e deve ser representada com uma linha tracejada ou pontilhada;
Uma curva de nível sempre tem um fim, seja fechando-se em si mesma, dentro ou fora dos limites do papel;
Uma curva de nível não pode bifurcar-se;
Terrenos planos apresentam curvas de nível mais espaçadas; em terrenos acidentados as curvas de nível encontram-se mais próximas uma das outras.
A representação de um terreno mediante o emprego das curvas de nível, deve ser um reflexo fiel do próprio terreno.

Às vezes, é necessário observar detalhadamente a variação do relevo de um terreno. Para isso, deve-se construir um perfil topográfico. Com base nas curvas de nível podemos construir perfis topográficos do relevo.
O perfil topográfico é uma representação gráfica de um corte vertical do terreno segundo uma direção previamente escolhida e pode ter diversas aplicações como na delimitação de áreas; na construção de estradas, edifícios, barragens; urbanização, saneamento e loteamentos; construção de canais de irrigação, pontes, túneis, viadutos; planejamento de linhas de transmissão e eletrificação, etc.
A construção de um perfil topográfico compreende as seguintes etapas:
1) Sobre o mapa topográfico traça-se uma reta, que corresponde à seção transversal do perfil que pretende-se construir;
2) Coloque sobre o mapa uma folha de papel milimétrico ou quadriculado de maneira que o eixo horizontal sobre o qual se vai construir o perfil seja paralelo à linha reta que foi traçada no mapa;
3) Projeta-se sobre o eixo horizontal a intersecção de cada curva de nível com a linha reta, tendo em conta a cota de altitude correspondente;
4) Traça-se um eixo vertical, que representa a altitude ou cotas;
5) Recorrendo ao eixo vertical localiza-se e marca-se o valor de cada curva de nível projetada;
6) Depois de marcados, unem-se todos os pontos correspondentes às curvas de nível projetadas dando origem a um perfil topográfico.
O perfil topográfico indicará as sinuosidades existentes no segmento escolhido.

Fonte:
http://educacao.uol.com.br/geografia/ult1701u95.jhtm
Curva de Nível
Por Caroline Faria
A curva de nível é uma maneira de se representar graficamente as irregularidades, ou o relevo, de um terreno.
Imagine uma montanha de 800 metros vista de cima. Seu formato é irregular, logo se traçarmos uma linha contornando-a a 700 metros o desenho do contorno (uma curva) será diferente, e menor, daquele que fizermos contornando-a a 100 metros, mais próximo da base. Esse desenho do contorno a uma dada altitude, que deve ser a mesma em todos os pontos da linha, é a chamada curva de nível e serve para representar o relevo de algum local nas plantas topográficas.
Geralmente, em uma planta topográfica, usa-se como referência a altura média do mar para se traçar as curvas de nível chamadas de “mestras” que são representadas por traços mais grossos. Podemos usar também, as linhas chamadas de auxiliares ou intermediárias para facilitar a leitura da planta topográfica. Todas as curvas possuem também, a altura em que se situam.
As curvas de nível são sempre paralelas entre si. Uma linha mestra jamais se cruzará com uma linha intermediária, por exemplo, mesmo que elas às vezes, cheguem bastante perto disso, e elas sempre se fecham sobre si mesmas (como um “O”, mas, na maioria das vezes, irregular). O que pode acontecer é de no papel, por causa de um efeito visual, as linhas se cruzarem, mas, na verdade, elas nunca se cruzam, uma vez que na realidade uma está embaixo da outra visto que cada curva de nível representa uma altitude. Nestes casos, costuma-se representar a linha, ou curva, debaixo com um tracejado.
Pela proximidade das linhas pode-se verificar se o terreno tem um declive muito acentuado ou não. Se as linhas estiverem muito próximas entre si, significa que o declive é bastante acentuado (um pico, por exemplo), já se elas estiverem muito distantes entre si, significa que o declive é suave (uma planície com pequenas elevações, por exemplo).
Mas, as curvas de nível não servem apenas para representar montanhas ou elevações no terreno. Se em uma planta topográfica com curvas de nível os valores da altitude referentes às curvas centrais forem menores do que os valores de altitude das curvas externas, significa que ali está representada uma depressão.
Quando se vai fazer uma planta topográfica com curvas de nível, costuma-se primeiro, antes de desenhar as curvas, fazer o traçado da rede de drenagem do terreno com o fim de facilitar o desenho das curvas. Afinal, é a rede de drenagem (rios, ribeirões, riachos, cachoeiras…) que determina, de forma geral, a topografia do terreno.
Outro conceito associado às curvas de nível (mas que não deve ser confundido) é o “plantio em curvas de nível”. Trata-se de uma técnica para plantio em terrenos acidentados que segue o traçado das curvas.
Lembrando que a legislação ambiental brasileira proíbe o desmate e plantio em terrenos com declividade maior que 45° por se tratar de Áreas de Preservação Permanente (APP) devido a alta tendência a erosão, o plantio em curvas de nível é uma técnica quer visa diminuir a velocidade da enxurrada (arraste) e aumentar a infiltração da água no solo para, com isso, evitar que aconteçam erosões.
Fontes
http://www.ibge.gov.br
http://www.ceplac.gov.br
http://educacao.uol.com.br
Origem do texto:
http://www.infoescola.com/cartografia/curva-de-nivel/



Nenhum comentário:
Postar um comentário